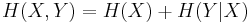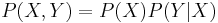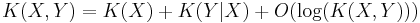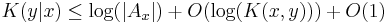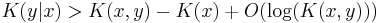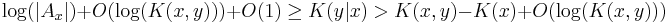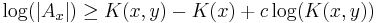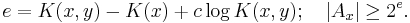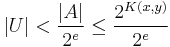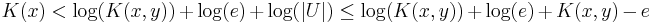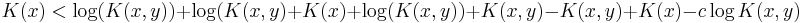Chain rule for Kolmogorov complexity
The chain rule for Kolmogorov complexity is an analogue of the chain rule for information entropy, which states:
That is, the combined randomness of two sequences X and Y is the sum of the randomness of X plus whatever randomness is left in Y once we know X. This follows immediately from the definitions of conditional and joint entropy fact from probability theory that the joint probability is the product of the marginal and conditional probability:
The equivalent statement for Kolmogorov complexity does not hold exactly; it is only true up to a logarithmic factor:
(An exact version, KP(X, Y) = KP(X) + KP(Y|X*) + O(1), holds for the prefix complexity KP, where X* is a shortest program for X.)
It states that the shortest program to reproduce X and Y is using a program to reproduce X and a program to reproduce Y given X, plus at most a logarithmic factor. Using this statement one can define an analogue of mutual information for Kolmogorov complexity.
Proof
The ≤ direction is obvious: we can write a program to produce x and y by concatenating a program to produce x, a program to produce y given access to x, and (whence the log term) the length of one of the programs, so that we know where to separate the two programs for x and y|x (log(K(x, y)) upper-bounds this length).
The ≥ direction is rather more difficult. The key to the proof is the construction of the set 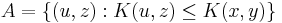 ; that is, the construction of the set of all pairs
; that is, the construction of the set of all pairs 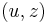 such that the shortest input (for a universal Turing machine) that produces
such that the shortest input (for a universal Turing machine) that produces 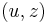 (and some way to distinguish
(and some way to distinguish  from
from  ) is shorter than the shortest producing
) is shorter than the shortest producing 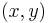 . We will also need
. We will also need 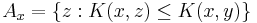 , the subset of
, the subset of  where
where 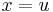 . Enumerating
. Enumerating  is not hard (although not fast!). In parallel, simulate all
is not hard (although not fast!). In parallel, simulate all 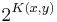 programs with length
programs with length 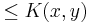 . Output each
. Output each 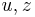 as the simulated program terminates; eventually, any particular such
as the simulated program terminates; eventually, any particular such 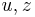 will be produced. We can restrict to Ax simply by ignoring any output where
will be produced. We can restrict to Ax simply by ignoring any output where 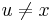 . We will assume that the inequality does not hold and derive a contradiction by finding a short description for K(x) in terms of its index in the enumeration of a subset of A.
. We will assume that the inequality does not hold and derive a contradiction by finding a short description for K(x) in terms of its index in the enumeration of a subset of A.
In particular, we can describe y by giving the index in which y is output when enumerating Ax (which is less than or equal to |Ax|) along with x and the value of K(x, y). Thus,
where the O(1) term is from the overhead of the enumerator, which does not depend on x or y.
Assume by way of contradiction
for some 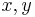 .
.
Combining this with the above, we have
So for any constant c and some x, y,
Let
Now, we can enumerate a set of possible values for  by finding all
by finding all  such that
such that 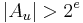 -- list only the
-- list only the  such that
such that  is output after more than
is output after more than 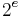 other values when enumerating
other values when enumerating 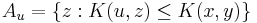 .
.  is one such
is one such  . Let
. Let  be the set of all such
be the set of all such  . We can enumerate
. We can enumerate  by enumerating each
by enumerating each 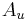 (in parallel, as usual) and outputting a
(in parallel, as usual) and outputting a  only when
only when  would be output for
would be output for 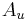 and more than
and more than 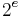 other values for the
other values for the 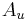 would be output. Note that given
would be output. Note that given 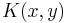 ,
,  and the index of
and the index of  in
in  we can enumerate
we can enumerate  to recover
to recover  .
.
Note that 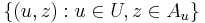 is a subset of
is a subset of  , and
, and  has at most
has at most 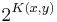 elements, since there are only that many programs of length
elements, since there are only that many programs of length 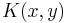 . So we have:
. So we have:
where the first inequality follows since each element of  corresponds to an
corresponds to an 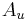 with strictly more than
with strictly more than 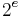 elements.
elements.
But this leads to a contradiction:
which when we substitute in  gives
gives
which for large enough  gives
gives 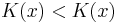 .
.
References
- Li, Ming; Vitányi, Paul (1997). An introduction to Kolmogorov complexity and its applications. New York: Springer-Verlag. ISBN 0387948686.